

We can see that the function goes all the way to negative infinity so: (-infinity. Let's determine the domain of the piecewise function. The graph above is missing labels and arrows. We would then label the pieces of our piecewise function. We would put a closed dot at x=2 and an arrow on the other end. We would put an open dot at x=2 for the parabola and an arrow on the other end. Then, we would erase any of the parabola showing after x=2. We would draw the parabola first and then the line. If we couldn't already see the graph, we would begin by examining the equation. This is very important as it makes the function a function. But, y = x² has just a "less than" sign which indicates that the circle at 2 will be open. The "equal to" indicates that the line y=-1 will have a closed dot at 2. Notice that we use a "greater than or equal to" sign for the horizontal line's domain. So the parabola would be denoted as y=x², x2 But, the parabola ceases to exist at x=2. The parabola is the parent parabola y=x². Let's begin with the parabola since it is furthest left.
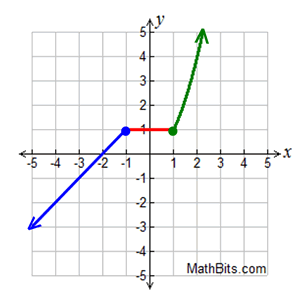
Let's write an equation for the piecewise function to the left, then walk through how we would graph it, and then determine the domain and range. Always check at the end to ensure that your function is a function. When graphing, try graphing the lines first, then erase and make dots and arrows as dictated by the domain (the x value behind the comma). Notice that the domain is determined by the comma and the x notation afterwards. If we were to write an equation for the graph to the right, it would look like this:

You'll notice that only (2,6) is actually included in the domain. If the dot is open, the coordinate is excluded, if it is closed than it is included. This is when closed and open dots come back into play from our domain graphs (see Project 1, page 2). But, we know that can't be the case or this wouldn't be a function. Assuming that each box is one unit, it appears that at an x value of 2, there are three different pieces of the function overlapping. Look at the piecewise function to the right. You'll notice that although there can be several different pieces, we must be careful not to have several outputs (y values) belonging to a single input (x value). In the example above, the range would be given by $[0,\infty)$.A piecewise function is a function that is in pieces. The range, in a similar way, is the set of all output values (i.e., heights) produced by the function. So in the example above, the domain would be $[-5,\infty)$. The domain of the piecewise-defined function is the set of all $x$ values that: 1) satisfy one of its various conditions, and 2) produce some (real-valued) output. Likewise, to indicate that the point where $x=3$ should be excluded from the linear piece (given the strict inequality), we place an open circle at $(3,1)$. Note, that we use a filled-in point at $(3,4)$ to suggest that the output of the function at $x=3$ is determined by the semi-circular piece - since the condition on this piece is true when $x=3$. Then, we discard those points that don't match the conditions provided (i.e., the dashed parts of the left graph below), to arrive at the graph of the piecewise-defined function on the right. We find its graph by first graphing $y = \sqrt$ (a semi-circle with center at the origin and radius 5) and $y=2x-5$ (a line of slope 2 with $y$-intercept at $(0,-5)$), as shown at left below. Graphing a piecewise function can be accomplished by simply graphing the functions found in the respective "pieces", limiting the points drawn for each piece to the $x$-values that satisfy the appropriate condition.
Graphing piecewise functions how to#
Thus, we summarize how to calculate the output with the following "piecewise definition": Multiplying a value by negative one has the same effect - so we can say that for this second piece $|x| = -x$. However, when $x \lt 0$, the absolute value changes the sign of its input. When $x \ge 0$, the absolute value function doesn't really do anything - it returns its input unchanged. When one creates a new function from existing functions in a "piecewise-defined" way, one breaks apart some domain into two or more disjoint pieces, using different functions to calculate the output for each $x$-value, where the function used is based upon the piece into which that particular $x$-value falls.Ī simple example of a piecewise defined function is the absolute value function, $|x|$.
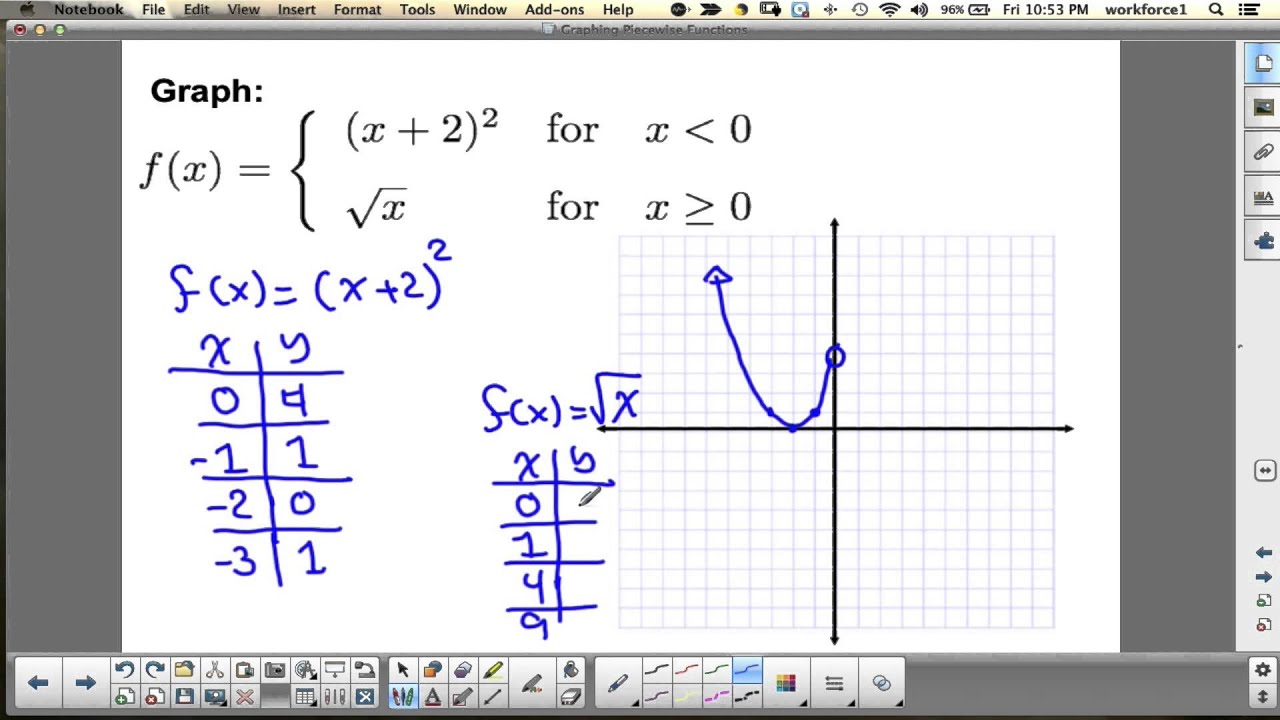
We can create new functions from existing ones in several ways.


 0 kommentar(er)
0 kommentar(er)
